O cenário: Estatística inferencial. O problema:

• Estamos considerando uma variável aleatória Y,
• Estamos interessados em determinado parâmetro (por exemplo, a média) associado a esta variável aleatória Y,
• Nós não sabemos o valor do parâmetro.

Assim:

1. Nós iremos estimar este parâmetro desconhecido utilizando os dados obtidos em nossa pesquisa e
2. Iremos também verificar quão boa é nossa estimativa.

O primeiro objetivo é bem mais fácil do que o segundo. Veja só: se o parâmetro que temos a necessidade de estimar é a média de uma variável aleatória, nós podemos fazer isso a partir da média amostral. A média populacional, que também é chamada de Esperança, é apresentada como E(Y) ou µ. A média amostral, por sua vez, é apresentada como ȳ. Basicamente, é possível mostrar que a média amostral é o melhor estimador para média populacional. Ele é não-viesado e consistente. No entanto, é importante lembrar que o valor de µ nem sempre será o ȳ de uma amostra.

A ideia para o segundo objetivo é a seguinte: apesar de termos, tipicamente, apenas uma mostra em mãos quando a gente trabalha na vida real, o raciocínio que embasa a estatística frequentista depende de pensarmos a longo prazo. Ou seja, pensarmos em todas as possibilidades adequadas para amostras. A melhor amostra adequada é, sem dúvidas, uma amostra aleatória simples e o exemplo abaixo materializa isso:

Nossa turma 5 de Estatística aplicada está com as inscrições abertas. Clique aqui e aproveite.

Estamos interessados em estimar a média de horas dormidas por um grupo de calouros universitários. Em termos estatísticos µ= E(Y).

• Coletamos uma amostra de observações  y₁, y₂, … , y_n sobre esta variável,
• Calculamos a média amostral e
• Para verificar o quão boa a nossa estimativa foi, vamos olhar em todas as outras possíveis amostras.

Isto pede que …  

• A gente faça mais pesquisas e armazene os valores encontrados das diversas médias amostrais Ȳ_{n (repita o procedimento).}
• Esta nova variável Ȳ_n terá uma distribuição (em inglês, sampling distribution) e nos dirá o quão bom foi nosso método para estimar a média populacional a partir da média amostral.

Nós não sabemos exatamente de Ȳ_n, pois depende de µ e nós não temos. Porém, os pressupostos do modelos  frequentistas nos permitem entender o seguinte:

• Se especificamos uma probabilidade, nós podemos achar um número (por exemplo a) em que a probabilidade de Ȳ_n estar entre µ-a e µ+a é de 0.95. Muita atenção, não estamos falando da probabilidade do parâmetro (na estatística frequentista, µ é uma constante), mas de nossa estimativa!

Agora só há duas possibilidades:

1. A amostra que estamos trabalhando é uma das 95% que contem o parâmetro (µ)
2. A amostra que estamos trabalhando é uma das 5% que não contem o parâmetro

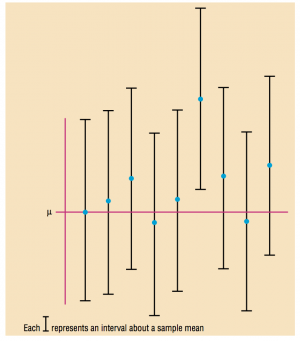(Imagem do livro Elementary Statistics, de Allan G. Bluman, 2012)